Future value (FV) is the valuation of an asset projected to the end of a particular time period in the future. You can calculate the future value of a lump sum or the future value of a series of deposits.
Future Value of a Lump Sum Equation (1.4) can be used to calculate the future value of a lump sum: FV (Present value of sum of money) (i 1.0)n (1.4) where i represents the interest rate and n represents the number of time periods. Applying this formula to our earlier example of investing $1000 at 8 percent for four years, we obtain
While mathematically correct, these calculations can be cumbersome when using long time periods. Table 1.1 provides a quick and easy way to determine the future dollar value of an investment. For the preceding example, use the table in the following manner: Go across the top row to the 8 percent column. Read down the 8 percent column to the row for four years to locate the factor 1.3605 (at the intersection of the green column and row). Multiply that factor by the present value of the cash asset ($1000) to arrive at the future value ($1360.50). Appendix Table A.1 provides an even more complete table for calculating the future value of lump-sum amounts. Figure 1.4 demonstrates the effects of various com-
pounded returns on a $10,000 investment. The $10,000 will grow to $57,435 in 30 years with an interest rate of 6 percent. Compounding $10,000 at 10 percent yields $174,494 over the same time period; at 14 percent, it yields a whopping $509,502! For practice you might want to confirm these results using Appendix Table A.1.
Rule of 72 Reveals Number of Years for Principal to Double The
rule of 72 is a handy formula for figuring the number of years it takes to double the principal using compound interest. You simply divide the interest rate that the money will earn into the number 72. For example, if interest is compounded at a rate of 7 percent per year, your principal will double in 10.3 years (72 7); if the rate is 6 percent, it will take 12 years (72 6). The rule of 72 (see Figure 1.5) also works for determining how long it would take for the price of something to double given a rate of increase in the price. For example, if college tuition costs were rising 8 percent per year, the cost of a college education would double in just over nine years. In addition, the rule of 72 can be used to calculate the number of years before prices will double given a certain inflation rate. Just divide the inflation rate into 72.
Future Value of an Annuity
Rule of 72 Reveals Number of Years for Principal to Double The
rule of 72 is a handy formula for figuring the number of years it takes to double the principal using compound interest. You simply divide the interest rate that the money will earn into the number 72. For example, if interest is compounded at a rate of 7 percent per year, your principal will double in 10.3 years (72 7); if the rate is 6 percent, it will take 12 years (72 6). The rule of 72 (see Figure 1.5) also works for determining how long it would take for the price of something to double given a rate of increase in the price. For example, if college tuition costs were rising 8 percent per year, the cost of a college education would double in just over nine years. In addition, the rule of 72 can be used to calculate the number of years before prices will double given a certain inflation rate. Just divide the inflation rate into 72.
Future Value of an Annuity
People often save for longterm goals by putting away a series of payments. Appendix Table A.3 provides a complete table for calculating the future value of a stream of deposited amounts, referred to as an annuity. Figure 1.6 graphically demonstrates the effects of various compounded returns on a $2000 annual investment made at the end of each year. The $2000 will grow to $91,524 in 20 years (read across the interest rate row in Appendix Table A.3 to 8 percent and then down the column to 20 years to obtain the factor of 45.762 to multiply by $2000) and to $226,566 in 30 years at an 8 percent rate. Compounding $2000 at 10 percent yields $114,550 in 20 years and $328,988 over 30 years; at 14 percent, it becomes $713,574 after 30 years! For practice you might want to confirm these results using Appendix Table A.3.

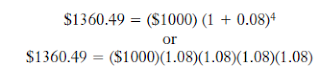


0 comments:
Post a Comment